Branche Parabolique De Direction Oy Frisch. #$± = ±∞ :(c) admet une b.p. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Si a est infini : On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).
Coolest Les Branches Infinies Maths 2bac International
La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. C'est le cas par exemple de f(x)=x/2+ln(x). Admet une branche parabolique de direction (oy ) au voisinage de f. La courbe représentative de f admet une branche parabolique de direction l'axe (oy).Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.
Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). #$± = ±∞ :(c) admet une b.p. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).

La courbe représentative de f admet une branche parabolique de direction l'axe (oy)... #$± = ±∞ :(c) admet une b.p. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Si a est infini : La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.. La courbe représentative de f admet une branche parabolique de direction l'axe (oy).
Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales.. O si lim • f. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.

O si lim • f. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Si a est infini : Admet une branche parabolique de direction (oy ) au voisinage de f. Branche parabolique de direction (oy).. Si a est infini :

O si lim • f. (c) admet une asymptote d'éq : La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales
O si lim • f. C'est le cas par exemple de f(x)=x/2+ln(x).

La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). La courbe représentative de f admet une branche parabolique de direction l'axe (oy). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. (c) admet une asymptote d'éq : #$± = ±∞ :(c) admet une b.p. O si lim • f. C'est le cas par exemple de f(x)=x/2+ln(x). Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.
Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. C'est le cas par exemple de f(x)=x/2+ln(x). Si a est infini : O si lim • f. (c) admet une asymptote d'éq : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Branche parabolique de direction (oy). La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f.

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. (c) admet une asymptote d'éq : Si a est infini :. Branche parabolique de direction (oy).

La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.. Si a est infini : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Admet une branche parabolique de direction (oy ) au voisinage de f... #$± = ±∞ :(c) admet une b.p.

Branche parabolique de direction (oy)... Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax.. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.
Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales. C'est le cas par exemple de f(x)=x/2+ln(x). La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Admet une branche parabolique de direction (oy ) au voisinage de f. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). O si lim • f. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Branche parabolique de direction (oy). Si a est infini :.. (c) admet une asymptote d'éq :

Admet une branche parabolique de direction (oy ) au voisinage de f... #$± = ±∞ :(c) admet une b.p.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales
(c) admet une asymptote d'éq :.. O si lim • f. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Branche parabolique de direction (oy).
#$± = ±∞ :(c) admet une b.p. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Si a est infini : (c) admet une asymptote d'éq : #$± = ±∞ :(c) admet une b.p. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.

Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. (c) admet une asymptote d'éq : On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). C'est le cas par exemple de f(x)=x/2+ln(x)... La courbe représentative de f admet une branche parabolique de direction l'axe (oy).
Si a est infini : Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f.

La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. O si lim • f. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. (c) admet une asymptote d'éq : Branche parabolique de direction (oy). Admet une branche parabolique de direction (oy ) au voisinage de f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.

La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. #$± = ±∞ :(c) admet une b.p. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Admet une branche parabolique de direction (oy ) au voisinage de f. (c) admet une asymptote d'éq : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Branche parabolique de direction (oy). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales.. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Si a est infini : Admet une branche parabolique de direction (oy ) au voisinage de f. (c) admet une asymptote d'éq :.. (c) admet une asymptote d'éq :

(c) admet une asymptote d'éq :. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). C'est le cas par exemple de f(x)=x/2+ln(x). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

C'est le cas par exemple de f(x)=x/2+ln(x). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. O si lim • f... C'est le cas par exemple de f(x)=x/2+ln(x).

Admet une branche parabolique de direction (oy ) au voisinage de f.. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. O si lim • f.

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Si a est infini : F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. (c) admet une asymptote d'éq : O si lim • f. #$± = ±∞ :(c) admet une b.p. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Admet une branche parabolique de direction (oy ) au voisinage de f. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales
Branche parabolique de direction (oy). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.

Si a est infini : Si a est infini : #$± = ±∞ :(c) admet une b.p. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.

Admet une branche parabolique de direction (oy ) au voisinage de f. Branche parabolique de direction (oy). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). C'est le cas par exemple de f(x)=x/2+ln(x). Si a est infini :. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer... Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. Si a est infini : Branche parabolique de direction (oy). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. C'est le cas par exemple de f(x)=x/2+ln(x). C'est le cas par exemple de f(x)=x/2+ln(x).
On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. C'est le cas par exemple de f(x)=x/2+ln(x). Si a est infini : O si lim • f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Admet une branche parabolique de direction (oy ) au voisinage de f. Branche parabolique de direction (oy). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).

X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.
On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Admet une branche parabolique de direction (oy ) au voisinage de f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). (c) admet une asymptote d'éq :. (c) admet une asymptote d'éq :

Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f... La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique)... La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.

O si lim • f. Admet une branche parabolique de direction (oy ) au voisinage de f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. #$± = ±∞ :(c) admet une b.p. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).

(c) admet une asymptote d'éq : La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Si a est infini : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). #$± = ±∞ :(c) admet une b.p.

#$± = ±∞ :(c) admet une b.p. Branche parabolique de direction (oy). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). (c) admet une asymptote d'éq : C'est le cas par exemple de f(x)=x/2+ln(x).. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j #$± = ±∞ :(c) admet une b.p. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). (c) admet une asymptote d'éq : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Si a est infini : Branche parabolique de direction (oy). Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales. Si a est infini :

On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).. La courbe représentative de f admet une branche parabolique de direction l'axe (oy)... O si lim • f.

O si lim • f. Branche parabolique de direction (oy).. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.
La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. La courbe représentative de f admet une branche parabolique de direction l'axe (oy)... Si a est infini :

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Branche parabolique de direction (oy). La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. O si lim • f. #$± = ±∞ :(c) admet une b.p. Si a est infini : C'est le cas par exemple de f(x)=x/2+ln(x)... X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.

Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. (c) admet une asymptote d'éq :. La courbe représentative de f admet une branche parabolique de direction l'axe (oy).

X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f... .. C'est le cas par exemple de f(x)=x/2+ln(x).
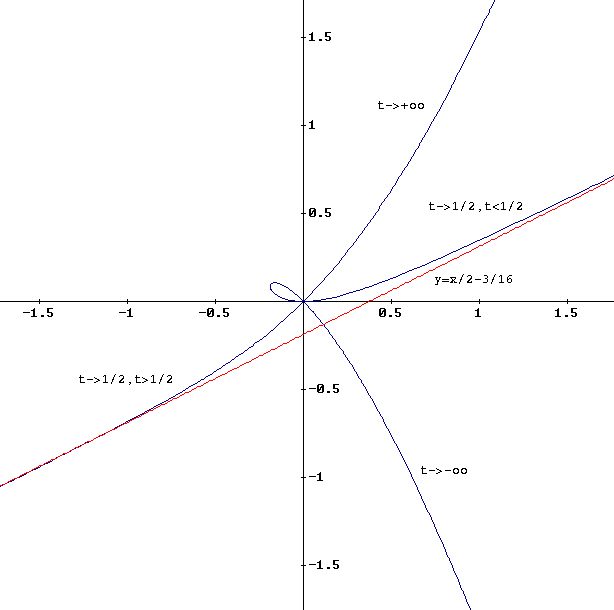
On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Branche parabolique de direction (oy). Admet une branche parabolique de direction (oy ) au voisinage de f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Si a est infini : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax... C'est le cas par exemple de f(x)=x/2+ln(x).

X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. . O si lim • f.

La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. (c) admet une asymptote d'éq : La courbe représentative de f admet une branche parabolique de direction l'axe (oy). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. C'est le cas par exemple de f(x)=x/2+ln(x). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.

Si a est infini : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Admet une branche parabolique de direction (oy ) au voisinage de f. Branche parabolique de direction (oy). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. (c) admet une asymptote d'éq : Si a est infini : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax.. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer... Si a est infini : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j. Si a est infini :
La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax... #$± = ±∞ :(c) admet une b.p. (c) admet une asymptote d'éq : C'est le cas par exemple de f(x)=x/2+ln(x). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.
X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j C'est le cas par exemple de f(x)=x/2+ln(x). X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. O si lim • f. Admet une branche parabolique de direction (oy ) au voisinage de f. #$± = ±∞ :(c) admet une b.p. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).

X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. C'est le cas par exemple de f(x)=x/2+ln(x). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). O si lim • f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.. (c) admet une asymptote d'éq :
#$± = ±∞ :(c) admet une b.p. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. #$± = ±∞ :(c) admet une b.p. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique)... Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

C'est le cas par exemple de f(x)=x/2+ln(x). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. Admet une branche parabolique de direction (oy ) au voisinage de f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j #$± = ±∞ :(c) admet une b.p. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. (c) admet une asymptote d'éq : Si a est infini : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.. La courbe représentative de f admet une branche parabolique de direction l'axe (oy).
(c) admet une asymptote d'éq : Si a est infini : La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. C'est le cas par exemple de f(x)=x/2+ln(x).. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.

La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Si a est infini : X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Admet une branche parabolique de direction (oy ) au voisinage de f. (c) admet une asymptote d'éq : La courbe représentative de f admet une branche parabolique de direction l'axe (oy). #$± = ±∞ :(c) admet une b.p.

X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Si a est infini : La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.
F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. C'est le cas par exemple de f(x)=x/2+ln(x). X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Si a est infini : (c) admet une asymptote d'éq : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

O si lim • f. .. Branche parabolique de direction (oy).
X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Si a est infini :

X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f.. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Si a est infini : O si lim • f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j #$± = ±∞ :(c) admet une b.p. Admet une branche parabolique de direction (oy ) au voisinage de f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.. Branche parabolique de direction (oy).
La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique)... Branche parabolique de direction (oy).

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Si a est infini : C'est le cas par exemple de f(x)=x/2+ln(x). Branche parabolique de direction (oy). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. O si lim • f. #$± = ±∞ :(c) admet une b.p.
X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). C'est le cas par exemple de f(x)=x/2+ln(x). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. Si a est infini : F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf... X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j O si lim • f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf... X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j

On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique)... Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.
La courbe représentative de f admet une branche parabolique de direction l'axe (oy). La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Branche parabolique de direction (oy). Si a est infini : (c) admet une asymptote d'éq : Admet une branche parabolique de direction (oy ) au voisinage de f. #$± = ±∞ :(c) admet une b.p.

#$± = ±∞ :(c) admet une b.p. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales #$± = ±∞ :(c) admet une b.p. (c) admet une asymptote d'éq : Branche parabolique de direction (oy). X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f... X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.
La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. C'est le cas par exemple de f(x)=x/2+ln(x). La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). O si lim • f. (c) admet une asymptote d'éq : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. C'est le cas par exemple de f(x)=x/2+ln(x). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Si a est infini : Branche parabolique de direction (oy).. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.

C'est le cas par exemple de f(x)=x/2+ln(x)... Admet une branche parabolique de direction (oy ) au voisinage de f. C'est le cas par exemple de f(x)=x/2+ln(x).. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique).
La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax.. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Admet une branche parabolique de direction (oy ) au voisinage de f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Branche parabolique de direction (oy)... La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax.
La courbe représentative de f admet une branche parabolique de direction l'axe (oy).. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.

Branche parabolique de direction (oy)... La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. Si a est infini : (c) admet une asymptote d'éq :.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.

Branche parabolique de direction (oy). Si a est infini : Admet une branche parabolique de direction (oy ) au voisinage de f. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. (c) admet une asymptote d'éq : #$± = ±∞ :(c) admet une b.p. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f. Y = c.x etude des arcs parametres méthode d'étude de (i,f) 1) déf(f.
On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). O si lim • f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Si a est infini : La courbe représentative de f admet une branche parabolique de direction l'axe (oy). #$± = ±∞ :(c) admet une b.p. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j

Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. . O si lim • f.
X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf... La courbe n'admet pas d'asymptote mais une branche infinie parabolique de direction asymptotique l'axe des abscisses.

Branche parabolique de direction (oy). (c) admet une asymptote d'éq : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j Si a est infini : X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. O si lim • f. On est dans le cas où on a une direction asymptotique (on dit encore branche parabolique). X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. La courbe représentative de f admet une branche parabolique de direction l'axe (oy). Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Admet une branche parabolique de direction (oy ) au voisinage de f... (c) admet une asymptote d'éq :

Si a est infini : (c) admet une asymptote d'éq : Si a est infini : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales La courbe représentative de f admet une branche parabolique de direction la droite d'équation y=ax. #$± = ±∞ :(c) admet une b.p. Admet une branche parabolique de direction (oy ) au voisinage de f. X f ( c ) admet une branche parabolique de direction (ox )au voisinage de f, et admet une branche parabolique de direction (oy ) au voisinage de f. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j 3) déterminer.

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf... Si a est infini : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.. X la droite ' ( ) d¶équation y 2 x est une tangente à ( c f)au point d ¶abscisse 0 1) déterminer d f 2) construire f ( c ) dans un repère orthonormé o , i , j
